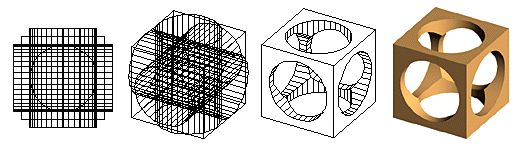
Considered by many the king of the solids modeling operations, Booleans in form·Z can be applied to both 2D shapes and 3D solids. They are complemented by the Trim and Stitch operations which can be applied to surfaces.

The unique ability of form·Z to apply Booleans to both 2D shapes and 3D solids allows you to mix the two as you model your designs. For example, you can start with basic 2D shapes, and then union or cut holes into them to derive a composite 2D shape. This shape can then be extruded or used by another operation to derive a 3D model. Or, you can begin with 3D solid primitives, and join or difference them directly as 3D solids.

Left: Boolean operation applied to 2D shapes to derive composite shapes, which are then extruded to derive 3D objects. Right: Boolean operations applied directly to 3D objects.

The Boolean operations in form·Z work, and can handle a variety of tricky cases where similar operations in other programs fail. Holes in particular are handled as true holes, and any number can be drilled into the same object.

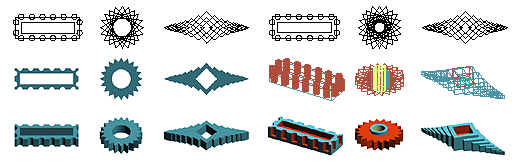
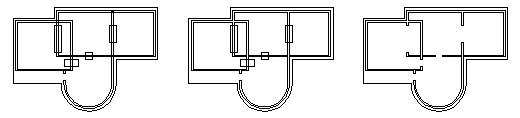
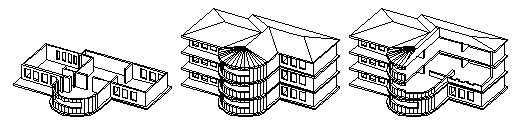
A benchmark case for Booleans: Three holes drilled in each of the three directions of a cube.

The Boolean operations are the most universal modeling operation, and offer powerful sculpting capabilities that architects, product designers, mechanical engineers, and designers from all professions can use with ease, as the examples that follow should clearly illustrate.

Using booleans for architectural modeling. Top to bottom, left to right: Rooms are first sketched as double line shapes. They are unioned and their openings are differenced to derive a unified floor plan. The plan and the base slab are extruded to derive the first floor, to which additional windows are opened directly in 3D. Three stories and a roof are erected and unioned. Using difference one part of the building is cut away to be able to see inside.

Mechanical parts and tools by Bruce Paterson, Marsden High School, Australia. They were all created through an extensive use of Boolean operations.

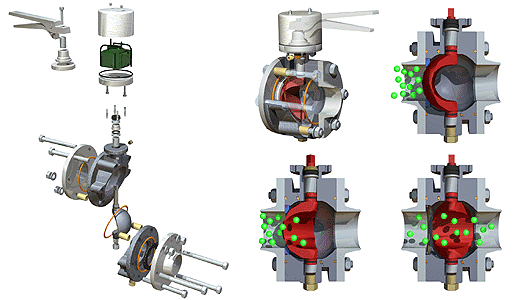
Omega Valve by Tim Reynolds, Blackpool and The Fylde College, Blackpool, Lancashire, England. form·Z models created through extensive use of booleans.